

|
Исходники
Статьи
Языки программирования
.NET Delphi Visual C++ Borland C++ Builder C/С++ и C# Базы Данных MySQL MSSQL Oracle PostgreSQL Interbase VisualFoxPro Веб-Мастеру PHP HTML Perl Java JavaScript Протоколы AJAX Технология Ajax Освоение Ajax Сети Беспроводные сети Локальные сети Сети хранения данных TCP/IP xDSL ATM Операционные системы Windows Linux Wap Книги и учебники
Скрипты
Магазин программиста
|
Эволюция мультиметодов при процедурном подходеОбъектно-ориентированное программирование позволяет реализовать эволюционный множественный полиморфизм. Однако тесная связь между методами и данными ведет к громоздкости интерфейсов в добавляемых классах, жесткому порядку их следования в эволюционной иерархии и невозможности повторного использования отдельных составляющих. Процедурный подход обеспечивает более гибкое расширение, как при добавлении данных, так и мультиметодов. ВведениеВ предыдущей статье [1] было показано, что ОО подход может поддерживать эволюционную разработку программ. Вместе с тем, следует отметить, что рассмотренные в ней приемы ведут к появлению жесткой связи между добавляемыми классами и к увеличению размера интерфейсов у потомков. Сохраняется также основной недостаток ОО подхода: появление новых методов (и мультиметодов) изменяет всю иерархию уже созданных классов. Процедурная реализация в целом выглядит более естественной. Вызов мультиметода по форме и содержанию эквивалентен вызову любой другой процедуры. Использование RTTI позволяет непосредственно проверять типы родственных объектов и обеспечивает вызов специализированных обработчиков. Иерархия классов при этом включает только методы, нацеленные на обработку внутренних данных. Отсутствуют какие-либо вспомогательные процедуры, осуществляющие дополнительное связывание: class Number {
public:
virtual void StdOut() = 0;
};
// Класс целых чисел.
class Int: public Number {
public:
void StdOut();
// Конструктор, обеспечивающий инициализацию числа.
Int(int v);
// Получение значения числа
int GetValue() {return _value;}
private:
// Значение целого числа
int _value;
};
// Класс действительных чисел.
class Double: public Number {
public:
// Вывод значения числа в стандартный поток
void StdOut();
// Конструктор, обеспечивающий инициализацию числа.
Double(double v);
// Получение значения числа
double GetValue() {return _value;}
private:
// Значение действительного числа
double _value;
};
Простота обработчиков альтернативных вариантов позволяет реализовать их непосредственно в теле функции вычитания: // Функция вычитания, использующая только RTTI.
Number* operator- (Number& n1, Number& n2) {
// Первый аргумент - целое число.
if(Int* pInt1 = dynamic_cast<Int*>(&n1)) {
// Второй аргумент - целое число.
if(Int* pInt2 = dynamic_cast<Int*>(&n2)) {
return new Int(pInt1->GetValue() - pInt2->GetValue());
}
// Второй аргумент - действительное число.
else if(Double* pDouble2 = dynamic_cast<Double*>(&n2)) {
return new Double(pInt1->GetValue() - pDouble2->GetValue());
}
}
// Первый аргумент - действительное число.
else if(Double* pDouble1 = dynamic_cast<Double*>(&n1)) {
// Второй аргумент - целое число.
if(Int* pInt2 = dynamic_cast<Int*>(&n2)) {
return new Double(pDouble1->GetValue() - pInt2->GetValue());
}
// Второй аргумент - действительное число.
else if(Double* pDouble2 = dynamic_cast<Double*>(&n2)) {
return new Double(pDouble1->GetValue() - pDouble2->GetValue());
}
}
}
Однако говорить об эволюции программы в данном случае не приходится. Параметризация обработчиков специализацийВ своем окончательном решении Скотт Мейерс тоже воспользовался внешними процедурами [2]. Однако его реализация опирается на моделирование таблицы виртуальных функций. Помимо этого используется ассоциативный доступ к обработчикам отдельных специализаций путем сравнения строк символов. Ниже предлагается вариант, обеспечивающий непосредственную индексацию функций, отвечающих за реализацию альтернативных составляющих. Основная специфика эволюционного расширения при процедурном подходе проявляется через независимость данных от функций, осуществляющих их обработку. Это позволяет отказаться от метафоры эволюционной пирамиды, заменив ее на волнообразное расширение методов, связанное с добавлением новых типов данных. 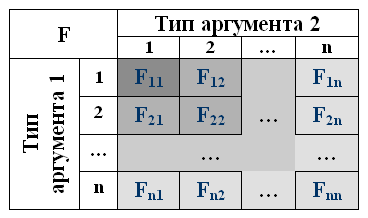 В принципе, подобное расширение можно осуществлять с использованием обычных структур данных. Однако сохраним классы, чтобы обеспечить более гибкую реализацию обычных виртуальных методов (например, функции вывода). Реализация волнообразного наращивания может опираться на непосредственное построение матрицы отношений между взаимодействующими классами. Как и в случае с прямой или реверсивной двойной диспетчеризацией [1], проблема индексации может быть решена применением специальной переменной класса, задающей его ранг в иерархии. Использование мультиметодов в качестве внешних процедур позволяет упростить организацию базового класса, определяющего общие параметры чисел: class Number {
public:
// Вывод значения числа в стандартный поток
virtual void StdOut() = 0;
// Конструктор, обеспечивающий установку ранга
Number(int r): _rank(r) {}
// Получить ранг класса
int GetRank() { return _rank;}
private:
// Число, задающее ранг класса
int _rank;
};
Конструирование всех производных классов осуществляется независимо друг от друга и по одинаковой схеме. Порядок следования этих классов в иерархии не влияет на их внутреннюю структуру, но затрагивает реализацию конструкторов и порядок реализации процедур, осуществляющих обработку отдельных альтернатив. Эти процедуры используются затем в мультиметодах. Начнем эволюцию с целочисленных данных. Соответствующий класс будет выглядеть следующим образом: // Класс целых чисел. Является первым в эволюции классов
class Int: public Number {
public:
void StdOut();
// Конструктор, обеспечивающий инициализацию числа.
Int(int v);
public:
// Значение целого числа
int _value;
};
Реализация методов является вполне традиционной. Необходимо только зафиксировать конкретный ранг класса в его конструкторе в соответствии с порядком следования в эволюционной иерархии // Ранг данного класса
const int intRank = 0;
// Конструктор, обеспечивающий инициализацию числа.
Int::Int(int v): Number(intRank), _value(v) {}
// Вывод значения числа в стандартный поток
void Int::StdOut() {
cout << "It is Int. Value = " << _value << endl;
}
Далее можно реализовать обработчик вычитания для уже существующих комбинаций. Пока – это вычитание целого числа из целого: // Обычное вычитание одного целого числа из другого
Int* SubIntInt(Int& n1, Int& n2) {
return new Int(n1._value - n2._value);
}
Для использования написанной функции в мультиметоде необходимо обобщить аргументы: // Обобщающее вычитание одного целого числа из другого.
Number* SubIntInt(Number& n1, Number& n2) {
Int* pInt1;
Int* pInt2;
// Динамическа проверка типа для исключения ошибок программиста
if( (pInt1 = dynamic_cast<Int*>(&n1)) &&
(pInt2 = dynamic_cast<Int*>(&n2)) ) {
// Оба типа соответствуют условиям проверки
return SubIntInt(*pInt1, *pInt2);
}
else {
// Ошибка в типах. Возможно формирование исключения.
return 0;
}
}
При формировании обобщающего вычитания можно обойтись и без динамической проверки типов: // Обобщающее вычитание одного целого числа из другого.
// Динамическая проверка типов отсутствует
Number* SubIntInt(Number& n1, Number& n2) {
return
SubIntInt(reinterpret_cast<Int&>(n1), reinterpret_cast<Int&>(n2));
// или:
//return SubIntInt((Int&)n1, (Int&)n2);
}
Однако в этом случае программист не гарантирован от ошибок при манипуляции указателями на полиморфные функции. Использование динамического типа рекомендовано в [2]. В качестве компромисса можно обратиться к препроцессору, который обеспечит динамическую проверку типов во время отладки и переключится на более быструю обработку при формировании окончательной версии программы. Аналогичные манипуляции проводятся при добавлении нового класса, например, действительного числа: class Double: public Number {
public:
void StdOut();
Double(double v);
public:
double _value;
};
Реализация методов должна учитывать установку в конструкторе нового ранга: // Ранг данного класса
const int doubleRank = 1;
// Конструктор, обеспечивающий инициализацию числа.
Double::Double(double v): Number(doubleRank), _value(v) {}
// Вывод значения числа в стандартный поток
void Double::StdOut() {
cout << "It is Double. Value = " << _value << endl;
}
Функции вычитания добавляются таким образом, чтобы обеспечить реализацию нового "фронта нарастающей волны": // Обычное вычитание одного действительного числа из другого
Double* SubDoubleDouble(Double& n1, Double& n2) {
return new Double(n1._value - n2._value);
}
// Обобщенное вычитание одного действительного числа из другого.
Number* SubDoubleDouble(Number& n1, Number& n2) {
Double* pDouble1;
Double* pDouble2;
// Динамическа проверка типа для исключения ошибок программиста
if( (pDouble1 = dynamic_cast<Double*>(&n1)) &&
(pDouble2 = dynamic_cast<Double*>(&n2)) ) {
// Оба типа соответствуют условиям
return SubDoubleDouble(*pDouble1, *pDouble2);
}
else {
// Ошибка в типах. Возможно формирование исключения.
return 0;
}
}
// Обычное вычитание действительного числа из целого
Double* SubIntDouble(Int& n1, Double& n2) {
return new Double(n1._value - n2._value);
}
// Обобщенное вычитание действительного числа из целого.
Number* SubIntDouble(Number& n1, Number& n2) {
Int* pInt1;
Double* pDouble2;
// Динамическа проверка типа для исключения ошибок программиста
if( (pInt1 = dynamic_cast<Int*>(&n1)) &&
(pDouble2 = dynamic_cast<Double*>(&n2)) ) {
// Оба типа соответствуют условиям
return SubIntDouble(*pInt1, *pDouble2);
}
else {
// Ошибка в типах. Возможно формирование исключения.
return 0;
}
}
// Обычное вычитание целого числа из действительного
Double* SubDoubleInt(Double& n1, Int& n2) {
return new Double(n1._value - n2._value);
}
// Обобщенное вычитание целого числа из дейсвтительного.
Number* SubDoubleInt(Number& n1, Number& n2) {
Double* pDouble1;
Int* pInt2;
// Динамическа проверка типа для исключения ошибок программиста
if( (pDouble1 = dynamic_cast<Double*>(&n1)) &&
(pInt2 = dynamic_cast<Int*>(&n2)) ) {
// Оба типа соответствуют условиям
return SubDoubleInt(*pDouble1, *pInt2);
}
else {
// Ошибка в типах. Возможно формирование исключения.
return 0;
}
}
Наличие у классов ранга, присутствие специализированных функций и их обобщенного интерфейса позволяют выстроить матрицу, задающую параметрические отношения между отдельными функциями вычитания и их операндами - специализациями. В качестве индексов, обеспечивающих выбор нужных функций, используются ранги экземпляров классов. Матрица содержит указатели на функции вычитания с одинаковыми сигнатурами: Number* SubXXX(Number& n1, Number& n2); Она может "видеть" только прототипы функций и "ничего не знать" об их реализации: // Функция полученная при добавлении к программе первого класса
Number* SubIntInt(Number& n1, Number& n2);
// Функции полученные при добавлении к программе второго класса
Number* SubIntDouble(Number& n1, Number& n2);
Number* SubDoubleInt(Number& n1, Number& n2);
Number* SubDoubleDouble(Number& n1, Number& n2);
// Количество классов
int const numbers = 2;
// Общее описание типа обобщающих функций
typedef Number* (*SubFunPtr)(Number& n1, Number& n2);
// Матрица мультиметодов
static SubFunPtr subtMatr[numbers][numbers] =
{
// Добавлено при создании первого класса
SubIntInt,
// Добавлено при создании второго класса
SubIntDouble, SubDoubleInt, SubDoubleDouble
};
Окончательное сокрытие реализации обеспечивается дополнительной функций, реализующей интерфейс с клиентом: // Функция вычитания, использующая множественный полиморфизм.
Number* operator- (Number& n1, Number& n2)
{
SubFunPtr fun = subtMatr[n1.GetRank()][n2.GetRank()];
if(fun) // Проверка на присутствие функции
return fun(n1, n2);
else
return 0; // или генерация исключения
}
Клиентская программа выглядит так же, как и при ОО подходе [1]: // Маленький тест.
void main() {
Number* rez;
Int i1(10); cout << "i1 = "; i1.StdOut();
Int i2(3); cout << "i2 = "; i2.StdOut();
Double d1(3.14); cout << "d1 = "; d1.StdOut();
Double d2(2.7); cout << "d2 = "; d2.StdOut();
rez = i1 - i2; cout << "i1 - i2 = "; rez->StdOut(); delete rez;
rez = d1 - d2; cout << "d1 - d2 = "; rez->StdOut(); delete rez;
rez = i1 - d2; cout << "i1 - d2 = "; rez->StdOut(); delete rez;
rez = d1 - i1; cout << "d1 - i1 = "; rez->StdOut(); delete rez;
}
Преодоление проблемы "общих знаний"Лобовое решение допускает эволюционное написание отдельных классов, но не спасает от объединения разрозненных знаний в одном месте. Это происходит при окончательном формировании матрицы отношений между операндами. В идеале хотелось получить такое решение, которое бы обеспечило независимое добавление как мультиметодов, так и классов, поддерживая, тем самым, не только эволюционное расширение, но и повторное использование. Добавление мультиметодов, при процедурном подходе, изначально осуществляется без модификации кода, так как функции находятся вне данных. "Развязать" добавление классов можно в том случае, если удастся обеспечить их независимость от значения ранга. Это можно сделать применением автоматического ранжирования во время запуска программы. Используем класс Number для подсчета числа производных классов, что будет также указывать на максимальный ранг ( _max_rank ): class Number {
public:
virtual void StdOut() = 0;
// Получение ранга класса для использования
// в параметрических вычислениях
virtual int GetRank() = 0;
protected:
static int _max_rank; // Фиксирует максимальный ранг системы классов
};
Виртуальная функция GetRank() выдает значение ранга и переопределяется в наследниках. Ранг может храниться в статической переменной конкретного производного класса, обеспечивая, тем самым, общий ключ для всех его экземпляров. Производные классы не зависят друг от друга, разрабатываются и включаются в проект в любом порядке. Для большей независимости следует использовать различные единицы компиляции. // Класс целых чисел. Теперь может быть любым в эволюции
class Int: public Number {
public:
// Вывод значения числа в стандартный поток
void StdOut();
// Получение ранга
int GetRank();
// Конструктор, обеспечивающий инициализацию числа.
Int(int v);
public:
// Значение целого числа
int _value;
private:
static int _rank; // Ранг всех целых чисел
};
// Класс действительных чисел. Теперь может быть любым в эволюции
class Double: public Number {
public:
// Вывод значения числа в стандартный поток
void StdOut();
// Получение ранга
int GetRank();
// Конструктор, обеспечивающий инициализацию числа.
Double(double v);
public:
// Значение действительного числа
double _value;
private:
static int _rank; // Ранг всех действительных чисел
};
Реализацию методов также следует вынести в отдельные файлы. Кроме этого необходимо инициализировать ранг начальным значением, сигнализирующим об отсутствии регистрации (в данном случае используется отрицательное число). Регистрацию классов надо провести до начала выполнения основной программы. Она осуществляется посредством создания регистрационного экземпляра класса. Независимость от порядка инициализации и уникальность этого экземпляра осуществляется использованием образца Singleton, реализованного по Мейерсу [3] в виде статической переменной функции (правило 47). Для целочисленных величин рассматриваемое решение выглядит следующим образом: // Ранг целочисленного класса
int Int::_rank = -1;
// Вывод значения числа в стандартный поток
void Int::StdOut() {
cout << "It is Int. Value = " << _value << endl;
}
// Получение ранга класса
int Int::GetRank() {return _rank;}
// Конструктор
Int::Int(int v): _value(v) {
if(_rank == -1) _rank = _max_rank++;
}
// Функция, реализующая образец Singleton, обеспечивающий
// единственность регистрационного экземпляра и автоматическое
// его создание при первом обращении.
Int& GetRegInt() {
static Int regInt(0);
return regInt;
}
Ничем не отличается и реализация методов обработки действительных чисел: // Ранг действтельного класса
int Double::_rank = -1;
// Вывод значения числа в стандартный поток
void Double::StdOut() {
cout << "It is Double. Value = " << _value << endl;
}
// Получение ранга класса
int Double::GetRank() { return _rank; }
// Конструктор, обеспечивающий инициализацию числа.
Double::Double(double v): _value(v) {
if(_rank == -1) _rank = _max_rank++;
}
// Функция, реализующая образец Singleton, обеспечивающий
// единственность регистрационного экземпляра и автоматическое
// его создание при первом обращении.
Double& GetRegDouble()
{
static Double regDouble(0.0);
return regDouble;
}
Специфической особенностью программы является использование класса Matrix для формирования массива указателей на функции, осуществляющие альтернативные вычитания. Он поддерживает: вставку обработчиков специализаций, автоматическое изменение размерности матрицы при добавлении новых специализаций, получение указателя на функцию по рангам ее аргументов. Внутри класса, вместо матрицы, используется одномерный массив. // Общее описание типа обобщающих функций
typedef Number* (*FunPtr)(Number& n1, Number& n2);
class Matrix {
public:
// Вставка в матрицу очередного метода на место, указанное индексами
void Insert(FunPtr fun, int i, int j);
// Получение специализированной функции по ее индексам
FunPtr GetFun(int i, int j);
private:
// создание "матрицы" большей размерности и перенос в нее
// ранее накопленных данных
void Replace(int new_size);
public:
// Конструктор класса
Matrix(): _fun_matr(0), _size(0) {}
// Деструктор, осуществляющий очистку массива указателей на функции
~Matrix() {if(_fun_matr) delete[] _fun_matr;}
private:
// Массив указателей на специализированные мультиметоды вычитания
// Создается динамически (вместо матрицы)
FunPtr* _fun_matr;
// Текущий размер матрицы
int _size;
};
Следует отметить, что представленная реализация не является единственно возможной, а сама матрица может использоваться для любых мультиметодов, осуществляющих обработку двух аргументов и возвращающих такой же третий. Метод вычитания использует экземпляр матрицы, заполненной указателями на специализации. Как и при регистрации классов, для формирования матрицы до момента ее использования, используется образец Singleton в виде статической переменной функции. В ходе вычислений функция вычитания получает указатель на эту матрицу. // Вместо матрицы используется функция, обращающаяся к статически
// заданной матрице. Таким образом, реализуется образец Singleton,
// обеспечивающий единственность экземпляра и автоматическое
// создание при первом обращении.
Matrix& GetSubtMatr() {
static Matrix subtMatr;
return subtMatr;
}
// Функция вычитания, использующая множественный полиморфизм.
Number* operator- (Number& n1, Number& n2) {
Matrix& subtMatr = GetSubtMatr();
FunPtr tmp_fun = subtMatr.GetFun(n1.GetRank(), n2.GetRank());
if(tmp_fun) // Проверка на присутствие указателя
return tmp_fun(n1, n2);
else
return 0; // или генерация исключения
}
Заполнение матрицы осуществляется по мере подключения к проекту новых обработчиков специализаций, а механизм их независимой регистрации обеспечивает гибкость метода. Регистрация обработчиков во многом определяется последовательностью сборки проекта. Поэтому, ранг объектов может устанавливаться в произвольном порядке и модифицироваться при добавлении новых классов или изменении структуры проекта. Одновременно можно регистрировать произвольное число обработчиков специализаций. Однако здесь следует учитывать возможность их независимого использования. В примере все функции регистрируются раздельно, что позволяет в дальнейшем эффективно применять шаблоны. Следует также отметить, что регистрационная функция локализована путем размещения в неименованном пространстве имен. В связи с выше изложенным единица компиляции, описывающая вычитание одного целого числа из другого будет выглядеть следующим образом: #include "IntClass.h"
#include "Matrix.h"
// Доступ к регистрационному классу для целых чисел
Int& GetRegInt();
// Доступ к матрице мультиметодов
Matrix& GetSubtMatr();
// Специализированное (обычное) вычитание одного целого числа из другого
Int* SubIntInt(Int& n1, Int& n2) {
return new Int(n1._value - n2._value);
}
// Обобщающее вычитание одного целого числа из другого.
// При этом аргументы являются ссылками на базовый класс,
// чтобы обеспечить их общую параметризацию.
Number* SubIntInt(Number& n1, Number& n2) {
Int* pInt1; Int* pInt2;
// Динамическая проверка типа для исключения ошибок программиста
if( (pInt1 = dynamic_cast<Int*>(&n1)) &&
(pInt2 = dynamic_cast<Int*>(&n2)) ) {
// Оба типа соответствуют условиям
return SubIntInt(*pInt1, *pInt2);
} else {
// Ошибка в типах. Возможно формирование исключения.
return 0;
}
}
// Регистрация функции определяющей отношение вычитания
// между двумя целочисленными классами
namespace {
// Описание соответствующего класса
class regIntInt {
public:
// Конструктор, отвечающий за регистрацию
regIntInt() {
Int& regInt = GetRegInt();
// В соответствии с рангом класса осуществляется
// занесение регистрируемой функции в массив (вектор)
// указателей на специализации
int Int_rank = regInt.GetRank();
Matrix& subtMatr = GetSubtMatr();
subtMatr.Insert(SubIntInt, Int_rank, Int_rank);
}
};
// Использование регистрирующего класса
regIntInt IntIntFun;
} // namespace
Аналогичным образом, но в других единицах компиляции, реализовано вычитание двух действительных чисел, целого из действительного и действительного из целого. Монометод как частный случай мультиметодаИнтересна ситуация, когда количество аргументов мультиметода уменьшается до одного. В этом случае множественный полиморфизм становится эквивалентен объектно-ориентированному полиморфизму, а мультиметод вырождается в "монометод". Отличие лишь в том, что полиморфный метод Fi, при использовании ООП, просто "размазывается" по множеству таблиц виртуальных функций производных классов C1-Ck, обеспечивающих реализацию отдельных специализаций F1i-Fki. Пример, демонстрирующий реализацию объектного полиморфизма для пяти производных классов, приведен на рис. 1. 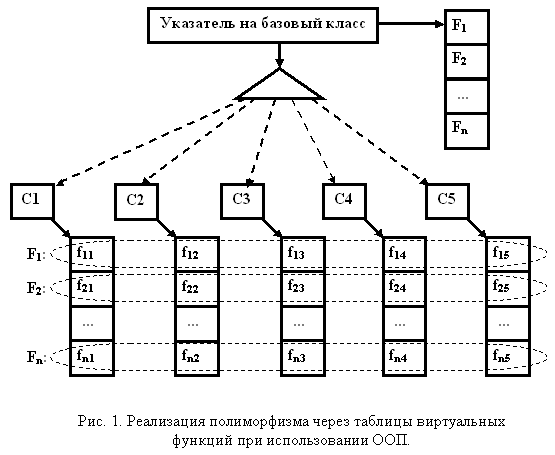 Процедурная версия монометода может опираться на размещение всех специализаций в едином одномерном массиве. Вызов альтернативы осуществляется в зависимости от ранга аргумента. В этом случае специализации Fi не прикрепляются к таблицам виртуальных функций отдельных классов, а располагаются независимо, что обеспечивает большую гибкость. Рис. 2, иллюстрирующий этот подход, также показывает, что ОО полиморфизм ортогонален процедурному по технической реализации. 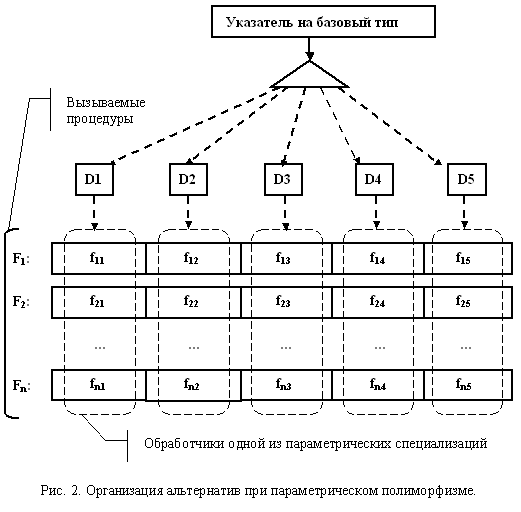 Построение монометода можно рассмотреть на примере функции вывода. Указатели на отдельные специализации хранятся в классе Vect, ориентированном на хранение векторов указателей. Использование класса vector из стандартной библиотеки шаблонов позволило упростить реализацию. // Задание типа обобщающих функций вывода
typedef void (*MonoFunPtr)(Number& n1);
class Vect {
public:
// Вставка в вектор очередного метода на место, указанное индексом
void Insert(MonoFunPtr fun, int i);
// Получение специализированной функции по ее индексу
MonoFunPtr GetFun(int i);
private:
// Для реализации вектора используется STL
vector
Обобщенный вывод опирается на вектор, параметризирующий соответствующие специализации, который имеется в одном экземпляре (Singleton). Функция обобщенного вывода Out выбирает специализацию по рангу выводимого класса. Ее действия полностью дублируют метод класса StdOut. // Вектор, параметризирующий функции вывода
Vect& GetOutVect() {
static Vect outVect;
return outVect;
}
// Функция вывода, использующая параметрический полиморфизм.
void Out(Number& n1) {
Vect& outVect = GetOutVect();
MonoFunPtr tmp_fun = outVect.GetFun(n1.GetRank());
if(tmp_fun) // Проверка на присутствие указателя
tmp_fun(n1);
else
; // или генерация исключения
}
Разработка специализаций и их регистрация осуществляются так же, как и при создании функции вычитания. Альтернатива, отвечающая за вывод целого числа, будет оформлена следующим образом: #include "IntClass.h"
#include "Vect.h"
// Доступ к регистрационному классу для целых чисел
Int& GetRegInt();
// Доступ к вектору мультиметодов
Vect& GetOutVect();
// Специализированный (обычный) вывод целого числа
void OutInt(Int& n1) {
cout << "It is Int. Value = " << n1._value << endl;
}
// Обобщающий вывод целого числа.
// При этом аргумент является ссылкой на базовый класс,
// чтобы обеспечить общую параметризацию.
void OutInt(Number& n1) {
Int* pInt1;
// Динамическа проверка типа для исключения ошибок программиста
if( (pInt1 = dynamic_cast<Int*>(&n1)) ) {
// Тип соответствует условиям
OutInt(*pInt1);
} else { // Ошибка в типах. Возможно формирование исключения.
;
}
}
// Регистрация функции определяющей вывод целого
namespace {
// Описание соответствующего класса
class regInt {
public:
// Конструктор, отвечающий за регистрацию
regInt()
{
Int& regInt = GetRegInt();
// В соответствии с рангом класса осуществляется
// занесение регистрируемой функции в массив (вектор)
// указателей на специализации
int Int_rank = regInt.GetRank();
Vect& outVect = GetOutVect();
outVect.Insert(OutInt, Int_rank);
}
};
// Использование регистрирующего класса
regInt IntFun;
} // namespace
Функция, обеспечивающая вывод значения действительного числа и ее регистрация осуществляются аналогичным образом. Разработанный монометод можно использовать вместо метода класса: void main()
{
Number* rez;
Int i1(10); cout << "i1 = "; Out(i1); // i1.StdOut();
Int i2(3); cout << "i2 = "; Out(i2); // i2.StdOut();
Double d1(3.14); cout << "d1 = "; Out(d1); // d1.StdOut();
Double d2(2.7); cout << "d1 = "; Out(d2); // d2.StdOut();
}
Его можно будет безболезненно наращивать при появлении новых классов. Приведенный пример показывает, что существует техническая реализация, ортогональная использованию виртуальным методам. Она является частным случаем множественного полиморфизма. Об инструментальной поддержке мультиметодовРассмотренный выше подход показывает принципы построения повторно используемых и эволюционно наращиваемых мультиметодов. Существуют различные трюки, расширяющие возможности этого кода и обеспечивающие его эффективное применение в реальных приложениях. Однако в рамках этой статьи мне хотелось бы затронуть несколько иную тему. Создание объектно-ориентированных языков программирования обеспечило инструментальную поддержку его трем основным китам: наследованию, инкапсуляции и полиморфизму. Отпала необходимость писать код, моделирующий соответствующие эффекты, что упростило создание безболезненно расширяемых программ и повторно используемых модулей. Вместе с тем все проблемы эволюционного программирования до конца оказались нерешенными и в частности, разработка мультиметодов. В статье показано, что существует достаточно простое техническое решение, которое может оказаться еще эффективнее, если его воплотить в соответствующих языковых и инструментальных средствах. В этом случае большая часть работы, связанной с регистрацией данных и функций ляжет на транслятор, а окончательное формирование параметрических отношений может проводиться во время статической или динамической компоновки, в крайнем случае, во время инициализации данных. В распоряжении программиста в этом случае окажется язык, позволяющий создавать функции, обеспечивающие поддержку множественного полиморфизма, а обычный полиморфизм, используемый в ОО языках программирования окажется его частным случаем. Возможность создания таких языков и построения на их основе процедурно-параметрической парадигмы программирования рассматривалась в работах [4-5]. В языке программирования Oberon, Н. Вирт успешно использовал механизм наследования для построения абстрактных типов данных. С. Мейерс [6] показал, что внешние функции улучшают инкапсуляцию. Я же попытался намекнуть, что расширение процедурных языков позволит поддерживать множественный полиморфизм, перекрывающий возможности ОО полиморфизма. Не существует технических причин безоговорочно верить в то, что эволюционная разработка, повторное использование кода, экстремальное программирование могут эффективно поддерживаться только ОО парадигмой. Литература
|
 Форум Программиста
Форум Программиста Новости
Новости Обзоры
Обзоры Магазин Программиста
Магазин Программиста Каталог ссылок
Каталог ссылок Поиск
Поиск Добавить файл
Добавить файл Обратная связь
Обратная связь |